Constructing a Volatility Surface
Introduction
A volatility surface maps out how implied volatility (IV) changes across different option strikes or deltas and expiration times, offering a three-dimensional view of the market’s expectation of future volatility. Constructing a volatility surface goes beyond merely collecting option prices and calculating IV’s. It involves selecting appropriate models, ensuring data integrity, selecting reasonable filters, and constantly updating to incorporate the latest market conditions. This task is pivotal for crafting informed trading strategies and pricing options effectively. However, the construction of a volatility surface is challenging due to its complexity and the precision required. The process demands a thorough mix of data analysis, model selection, and market comprehension, making it a demanding yet essential component of financial analytics.
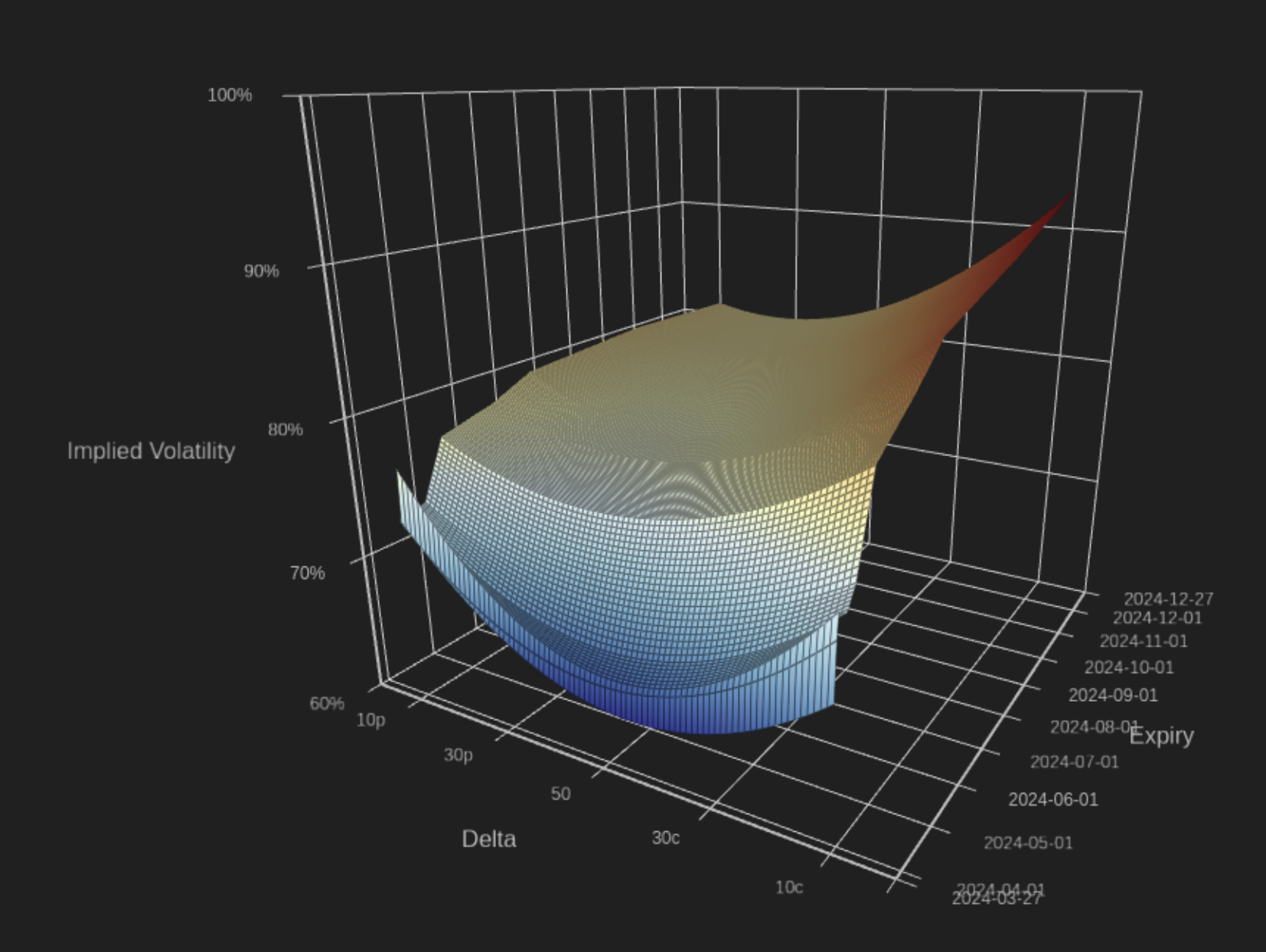
Figure 1: Visualization of a volatility surface for BTC.
Below, we outline the process used to create a volatility surface for Bitcoin and Ethereum, starting from raw data, and finishing with a delta-based volatility surface, an example of which can be seen in Figure 1. Our process is carried out separately for call and put options until the final step, where both are combined into a single volatility surface. First, we filter and process the raw data to remove any invalid or missing values. Next, instrument IVs are grouped by expiry, and we apply a more detailed filter on a per-expiry basis to exclude unwanted data points, and potentially exclude the entire expiry. After filtering, we fit the data for each expiry to a quadratic model, and interpolate the IV’s for each target delta. Grids are then constructed for calls and puts using bilinear interpolation to construct a regular grid for expiry steps of 1 day, and delta steps of 1 delta. Finally, we merge the grids for puts and calls into a single surface arranged according to how delta-based surfaces traditionally are.
Raw Data Processing
For this step and the majority of remaining steps, calls and puts are handled separately, and any differences in operations between the two will be specifically highlighted. We start with raw data from various venues that offer options on the underlying (BTC/ETH). This data is generally in the form of order book snapshots for the entire options chain from each venue, which includes data such as bids, asks, Greeks, IVs, mark IVs, mark prices, etc. At this point, only simple filtering is performed, namely filtering out any instruments that have missing data or zero values for required information such as price. Once this filtering has been performed, the next step is processing, where we compute a delta and IV for each instrument. These values can be computed in various ways, for example, using Black-Scholes. In some cases, venues provide values for delta, mark IV, etc., which can also be used as inputs to our model. It is important to note that at this stage, there may be multiple IV values for a single delta value.
Per-Expiry Filtering
Once a list of instruments has been built, including corresponding expiry, delta, and IV, we are ready to perform additional filtering on a per-expiry basis. Instruments are grouped by their expiry, then the following filters are applied for each instrument:
Any instruments with a delta outside the range [4, 96] are excluded. Entries outside of this range have a tendency to have extreme values which negatively impact the resulting volatility surface.
The standard deviation and mean of the IV is calculated, and any instruments with IVs that are more than two standard deviations away from the mean are excluded.
Once the per-instrument filters are applied, additional filters are introduced to potentially exclude an entire expiry. Specifically:
3. Any expiries which don’t contain at least one instrument with a delta less than 50, and one instrument with a delta greater than 50 are excluded. Cases like these often indicate an illiquid expiry.
4. Any expiries which have less than 4 instruments after filtering are excluded. This is based on the minimum number of points required to obtain a reasonable fit for our volatility model.
The end result of this is a list of expiries, each consisting of a list of instruments with delta and IV values.
Quadratic Model Fitting
Now that we have our filtered data, we are ready to begin constructing our surface. We begin by using least-squares to fit a quadratic to our data. A quadratic was selected as it provides a good combination of reasonableness and accuracy. For each expiry, we get a list of x and y pairs as the delta and IV of each instrument, and solve for the coefficients of x in ax2+bx+cax^2 + bx + cax2+bx+c. At this point, there is still the possibility for an expiry to be excluded. This occurs when the least-squares fit is badly conditioned, or when the calculated coefficients have unreasonable values.
Once we have a final list of expiries and corresponding quadratic models, we obtain an IV value by sampling each model at each target delta we have in the final surface, which in our case is every delta in the range [5, 95] in 1 delta increments. This gives us an irregular grid-based version of a volatility surface, with delta on the x-axis and being regular, expiry/tenor on the y-axis and being irregular, and IV on the z-axis.
Regular Grid Creation
In order to construct our final regular grid, we must determine which values to use for our y-axis. For our y-axis values, we choose floating tenors in 1 day intervals, starting at 8 AM UTC on the shortest expiry in our data, and ending at 8 AM UTC on the furthest expiry, which tends to be an end-of-year expiry. Other possibilities can include using different reference times such as 10 AM EST, or using constant tenors based on a user-defined fixed offset from the time the surface was generated.
Now that we have our regular grid, we make use of bilinear interpolation to calculate the IV at each point in our grid. It is possible to use other interpolation methods here, such as splines, but we found that bilinear is sufficient to produce reasonable and accurate surfaces, as well as limit any surprises such as spikes or jumps that can occur when using more complicated methods.
Final Surface Generation
Up to this point, we have been constructing two different surfaces, one for calls and puts. We now merge both surfaces following the traditional layout of a delta-based volatility surface. This consists of an x-axis with 10 delta calls on the left, moving to 50 delta in the center, and moving lower to 10 delta puts on the right.
Creating this final surface is fairly straightforward using simple data manipulation. One important thing to note is that the range of the y-axis (tenor) should be a range that is a subset of the ranges for calls and puts. For the 50 delta, we use the average of IVs for 50 delta from the calls and the puts surfaces. The end result can then be seen in Figure 2.
Figure 2: The final surface created by our process
Conclusion
Creating a volatility surface involves more than just compiling option prices and calculating IVs. It’s a detailed process that requires selecting the right models, proper tuning, ensuring data integrity, selecting reasonable filters, and constantly updating to keep pace with evolving market dynamics. The tools and techniques employed to build our volatility surface are highly adaptive. As a result, we are able to extrapolate and interpolate any of our models with granular resolution, for any specified date and expiry.